Composing Monadic Functions with Kleisli Arrows

Function composition is great isn’t it? It’s one of the corner-stones of Functional Programming. Given a function g: A => B and a function f: B => C we can compose them (join them together) as f compose g to return a function A => C. The composition hides the intermediate steps of A => B and B => C, instead letting us focus on the initial input (A) and final output (C). This is the glue that lets us write many small functions and combine them into larger, more useful functions.

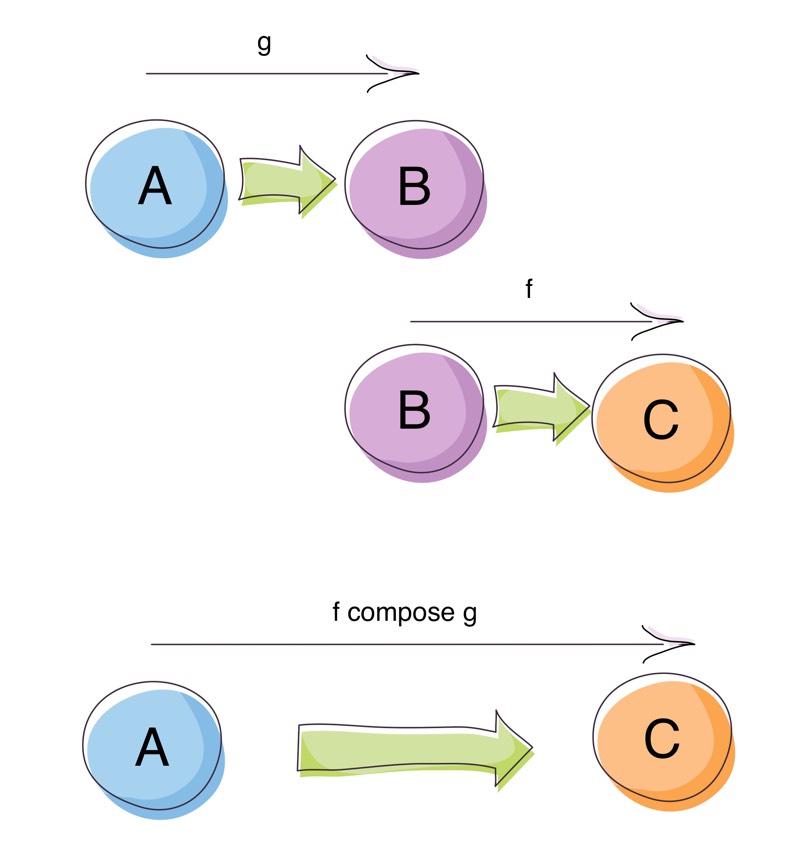
Function composition works from right to left, where the first function called is the one on the right. This can be confusing when learning about composition, as we are used reading from left to right. If you find this confusing you can use the andThen function instead which orders the functions from left to right: g andThen fas opposed to f compose g.

In this article we use the Scala language and the Cats functional programming library to illustrate the main concepts. The source code for this article is available on Github.

To make this more concrete with a simple example, lets start with the following functions:

  def mul2: Int => Int = _ * 2

  def power2: Int => Double = Math.pow(_, 2)

  def doubleToInt: Double => Int = _.toInt

  def intToString: Int => String = _.toString

While these simple functions work in isolation, we can also combine them (compose them) together to create a more powerful function that does what all of the functions do:

val pipeline: Int => String = intToString compose mul2 compose doubleToInt compose power2

pipeline(3)//returns "18"

The pipeline function, combines all the functions together to create a new function that:

Raises a supplied number to the power of 2
Converts the result to an Int value
Multiplies the result value by 2
Converts the result to a String

We can do this because the types align all the way down:

Int => Double //power2
       Double => Int //doubleToInt
                 Int => Int //mul2
                        Int => String //intToString

Int => String //pipeline

Now we can use and pass around the pipeline function without thinking about all the small functions comprise it.

Monadic Functions

Things get a little more interesting when we have functions that return values in a context:

  def stringToNonEmptyString: String => Option[String] = value =>
    if (value.nonEmpty) Option(value) else None

  def stringToNumber: String => Option[Int] = value =>
    if (value.matches("-?[0-9]+")) Option(value.toInt) else None

If we try to compose stringToNonEmptyString and stringToNumber:

val pipeline: String => Option[Int] = stringToNumber compose stringToNonEmptyString

we get the following compilation error:

[error]  found   : String => Option[String]
[error]  required: String => String
[error]     val pipeline: String => Option[Int] = stringToNumber compose stringToNonEmptyString

Oh dear! When we compose stringToNonEmptyString with stringToNumber, the stringToNumber function expects a String but instead stringToNonEmptyString is supplying it an Option[String]. The types don’t align any more and we can’t compose:

//the types don't align
String => Option[String] //stringToNonEmptyString
          String => Option[Int] //stringToNumber

It would be nice if we didn’t have to think about the context of the result type (Option[String] in this instance) and just continue to compose on the plain type (String in this instance).

Kleisli Composition

Kleisli is a type of Arrow for a Monadic context. It is defined as:

final case class Kleisli[F[_], A, B](run: A => F[B])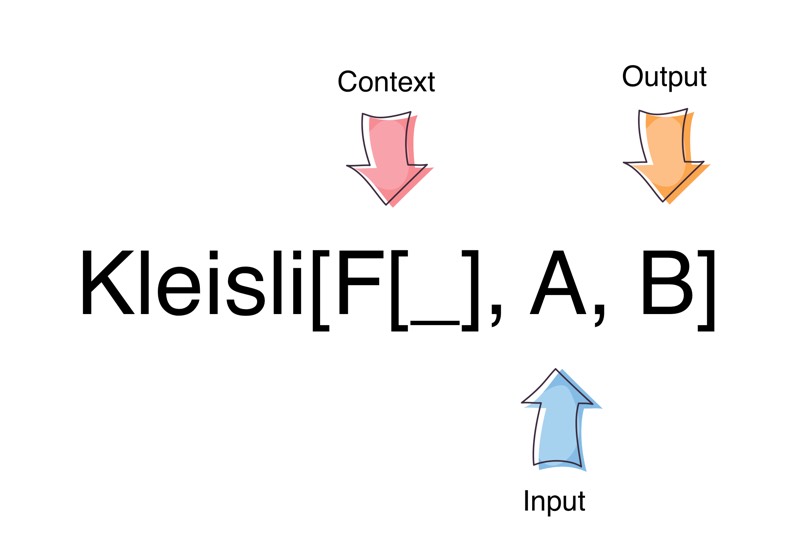

The Kleisli type is a wrapper around A => F[B], where F is some context that is a Monad. What helps us with our composition of contextual results, is that Kleisli has a compose function with the following signature (simplified for clarity):

def compose(g: A => F[B], f: B => F[C])(implicit M: Monad[F]): A => F[C]

What the above signature tells us is that we can join together functions that return results in a context F (for which we have a Monad instance) with functions that work on the simple uncontextualised value:

A => F[B] //g
       B => F[C] //f

A => F[C] //f compose g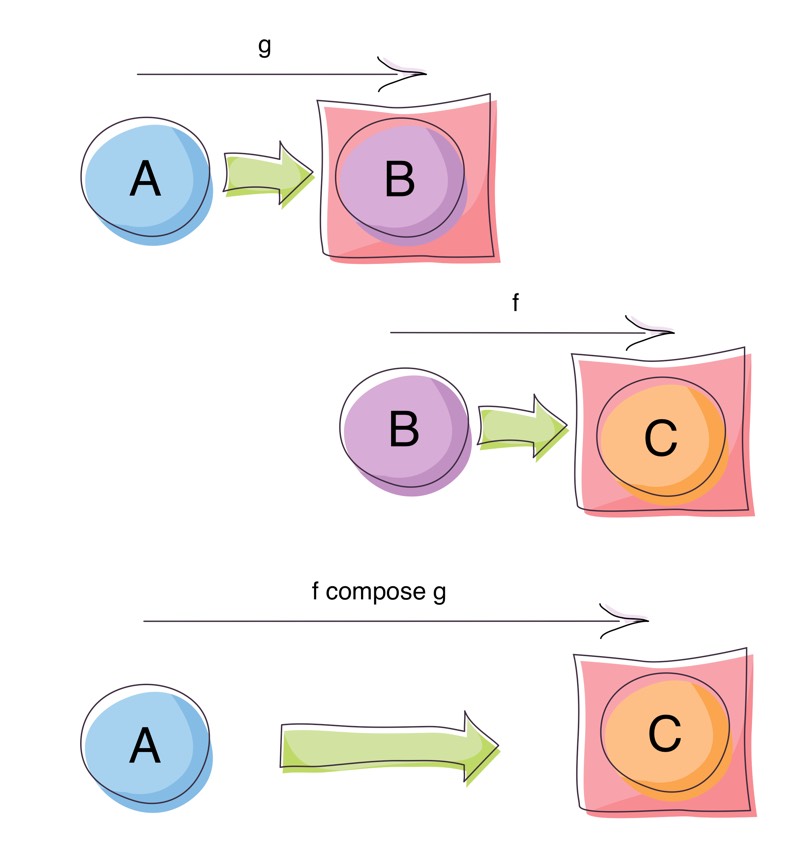

For the stringToNonEmptyString and stringToNumber functions, the Monadic context used is Option (both functions return an optional value).

So why does the Kleisli compose method need a Monadic instance for F? Under the covers Kleisli composition uses Monadic bind (>>=) to join together the Monadic values. Bind is defined as:

def bind[A, B](fa: F[A])(f: A => F[B]): F[B]

Using Kleisli Composition

Let’s try and compose the stringToNonEmptyString and stringToNumber functions again but this time using Kleisli composition:

import cats.data.Kleisli
import cats.implicits._ //Brings in a Monadic instance for Option

val stringToNonEmptyStringK = Kleisli(stringToNonEmptyString) //Kleisli[Option, String, String]
val stringToNumberK = Kleisli(stringToNumber) //Kleisli[Option, String, Int]

val pipeline = stringToNumberK compose stringToNonEmptyStringK //Kleisli[Option, String, Int]

pipeline("1000") //Some(1000)
pipeline("") //None
pipeline("A12B") //None

And now we can successfully compose the two functions! In addition, notice how when we use different inputs, the Monadic result changes; The same rules apply for composing these Monadic values through Kleisli composition as for Monadic bind. If a value of None is returned from one of the intermediate functions, the the pipeline returns a None. If all the functions succeed with Some values, then the pipeline returns a Some as well.

Using Plain Monads

Given that Kleisli composition, needs a Monadic instance to do its magic, could we simply replace Kleisli composition with straight Monads? Let’s give it a shot:

import KleisliComposition._
import cats.implicits._

val pipeline: String => Option[Int] = Option(_) >>= stringToNonEmptyString >>= stringToNumber
pipeline("1000") //Some(1000)
pipeline("")// None
pipeline("A12B")// None

Or if we have the input up front:

import cats.implicits._

Option("1000") >>= stringToNonEmptyString >>= stringToNumber //Some(1000)
Option("") >>= stringToNonEmptyString >>= stringToNumber //None
Option("A12B") >>= stringToNonEmptyString >>= stringToNumber //None

And it looks like we can.

Benefits of Kleisli Composition

So what does Kleisli Composition really give us over using plain old Monads?

Allows programming in a more composition like style.
Abstracts away the lifting of values into a Monad.

And if we squint, A => F[B] looks a lot like the Reader Monad. More on that later.