Java Planet Enum in Haskell
A while back I was trying to implement the Java Planet Enum example in Haskell. Below is the Java source taken directly from the Oracle documentation:
public enum Planet {
MERCURY (3.303e+23, 2.4397e6),
VENUS (4.869e+24, 6.0518e6),
EARTH (5.976e+24, 6.37814e6),
MARS (6.421e+23, 3.3972e6),
JUPITER (1.9e+27, 7.1492e7),
SATURN (5.688e+26, 6.0268e7),
URANUS (8.686e+25, 2.5559e7),
NEPTUNE (1.024e+26, 2.4746e7);
private final double mass; // in kilograms
private final double radius; // in meters
Planet(double mass, double radius) {
this.mass = mass;
this.radius = radius;
}
private double mass() { return mass; }
private double radius() { return radius; }
// universal gravitational constant (m3 kg-1 s-2)
public static final double G = 6.67300E-11;
double surfaceGravity() {
return G * mass / (radius * radius);
}
double surfaceWeight(double otherMass) {
return otherMass * surfaceGravity();
}
public static void main(String[] args) {
if (args.length != 1) {
System.err.println("Usage: java Planet <earth_weight>");
System.exit(-1);
}
double earthWeight = Double.parseDouble(args[0]);
double mass = earthWeight/EARTH.surfaceGravity();
for (Planet p : Planet.values())
System.out.printf("Your weight on %s is %f%n",
p, p.surfaceWeight(mass));
}
}This seemed fairly easy. I started off by modelling a Planet and associated data:
data Planet = MERCURY
| VENUS
| EARTH
| MARS
| JUPITER
| SATURN
| URANUS
| NEPTUNE deriving (Enum, Bounded, Show)
newtype Mass = Mass Double
newtype Radius = Radius Double
data PlanetStat =
PlanetStat {
mass :: Mass
, radius :: Radius
}
newtype SurfaceGravity = SurfaceGravity Double
newtype SurfaceWeight = SurfaceWeight Double
gConstant :: Double
gConstant = 6.67300E-11One difference between Haskell and OOP languages is that Haskell separates out data from behaviour while OOP languages combine data (or state) and behaviour into one construct - a class.
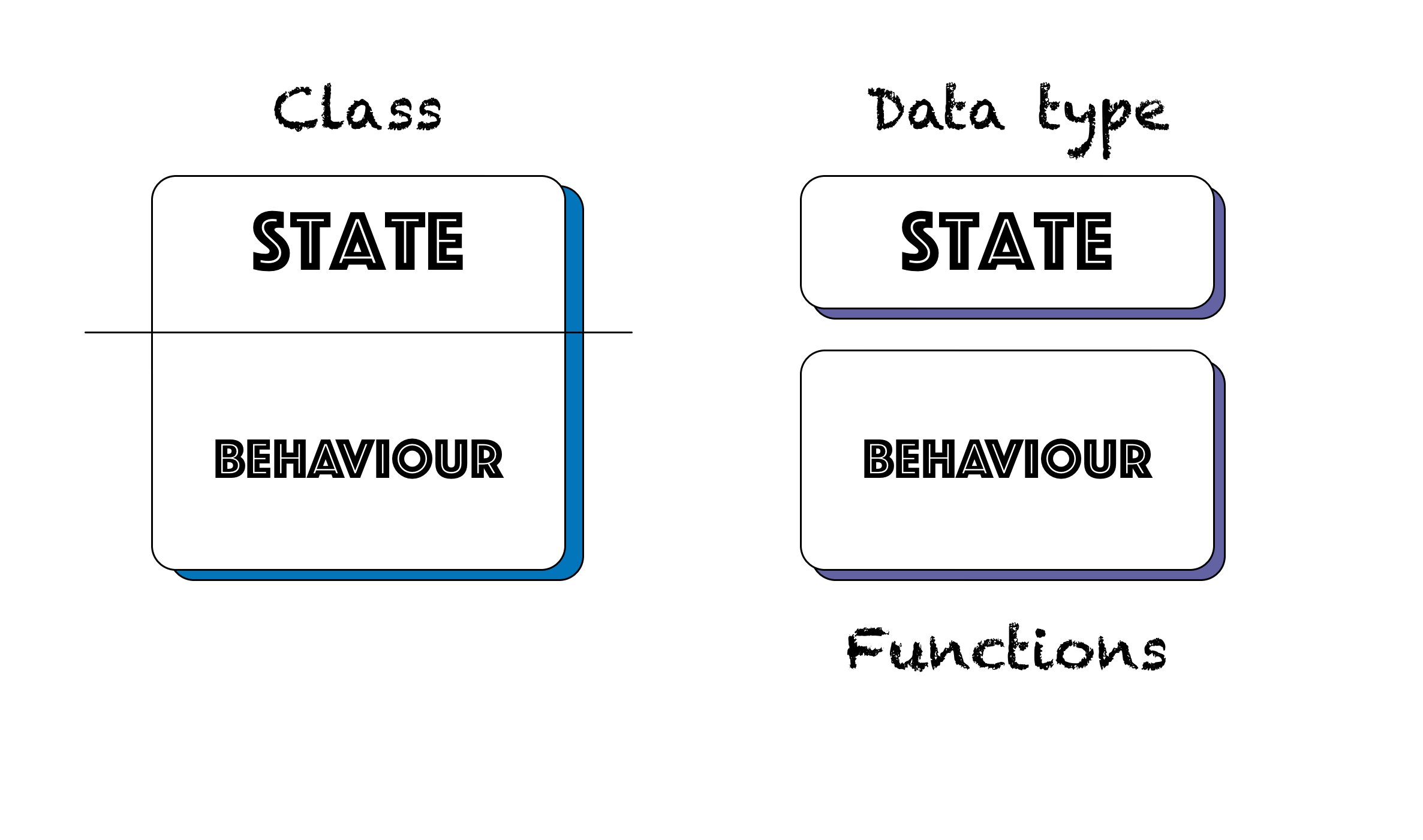
In Java, surfaceGravity and surfaceWeight are bound to a particular Planet instance. In Haskell, as mentioned above, we don’t have behaviour and state stored together. How do we go about implementing these functions in Haskell?
Instead of having state and behaviour combined, we can use the state to derive any behaviour we need:
surfaceGravity :: Planet -> SurfaceGravity
surfaceGravity planet =
let (PlanetStat (Mass mass) (Radius radius)) = planetStat planet
in SurfaceGravity $ gConstant * mass / (radius * radius)
surfaceWeight :: Mass -> Planet -> SurfaceWeight
surfaceWeight (Mass otherMass) planet =
let (SurfaceGravity sg)= surfaceGravity planet
in SurfaceWeight $ otherMass * sgNotice how we pass in the Planet instance we need to each function above. We don’t have a this reference as in most OOP languages. Here’s the Java implementation of the above functions with an explicit this reference added:
double surfaceGravity() {
return G * this.mass / (this.radius * this.radius);
}
double surfaceWeight(double otherMass) {
return otherMass * this.surfaceGravity();
}That solves one problem, but there’s another. It has to do with retrieving all the values of an enumeration. In the Java example we use:
Planet.values()How do we get all the values of an enumeration in Haskell?
You may have noticed the deriving (Enum, Bounded ...) syntax against the Planet data type. Using the Enum and Bounded type classes we can retrieve all the values of the Planet sum type:
planetValues :: [Planet]
planetValues = [(minBound :: Planet) .. (maxBound :: Planet)]The above code, grabs the first (minBound) and last (maxBound) values of the Planet sum type and the range syntax (..) makes it possible to enumerate all the values in between. Pretty nifty! The range syntax is made possible by having an Enum instance for a data type. See the enumFrom, enumFromThen, enumFromThenTo and enumFromTo functions on the Enum type class for more information.
It’s starting to look like we’ve got this solved pretty easily. Unfortunately we have another small problem. The planetValues function only gives us the Planet sum type - essentially the names of the planets. We also need to retrieve the mass and radius for each planet as per Java:
public enum Planet {
MERCURY (3.303e+23, 2.4397e6),
VENUS (4.869e+24, 6.0518e6),
EARTH (5.976e+24, 6.37814e6),
MARS (6.421e+23, 3.3972e6),
JUPITER (1.9e+27, 7.1492e7),
SATURN (5.688e+26, 6.0268e7),
URANUS (8.686e+25, 2.5559e7),
NEPTUNE (1.024e+26, 2.4746e7);
...How do we go about doing this?
We could create a Map with Planet as the key and PlanetStat as the value. So far so good. But when we go to look up a value we have to use the lookup function:
lookup :: Ord k => k -> Map k a -> Maybe aThe return type of the lookup function is a Maybe. This means we have to deal with the possibility of not finding a particular Planet (the Nothing case):
-- planetMap :: Map Planet PlanetStat
case (lookup somePlanet planetMap) of
Just planet -> -- cool planet-related stuff
Nothing -> -- this should never happen!We know this is impossible because we have a sum type for Planet, but because we are using a Map we need to deal with it.
Another way to encode this mapping is like this:
planetStat :: Planet -> PlanetStat
planetStat MERCURY = PlanetStat (Mass 3.303e+23) (Radius 2.4397e6 )
planetStat VENUS = PlanetStat (Mass 4.869e+24) (Radius 6.0518e6 )
planetStat EARTH = PlanetStat (Mass 5.976e+24) (Radius 6.37814e6)
planetStat MARS = PlanetStat (Mass 6.421e+23) (Radius 3.3972e6 )
planetStat JUPITER = PlanetStat (Mass 1.9e+27 ) (Radius 7.1492e7 )
planetStat SATURN = PlanetStat (Mass 5.688e+26) (Radius 6.0268e7 )
planetStat URANUS = PlanetStat (Mass 8.686e+25) (Radius 2.5559e7 )
planetStat NEPTUNE = PlanetStat (Mass 1.024e+26) (Radius 2.4746e7 )This way we don’t have to deal with any optionality; this is a total function.
It’s interesting that Java gives us this mapping for “free” because it combines state and behaviour. In Haskell you need to bring state and behaviour together as required. A big thanks to my friend Adam for pointing this out. In hindsight it seems obvious.
And that’s about it for surprises. Here’s the full solution:
import Data.Foldable (traverse_)
data Planet = MERCURY
| VENUS
| EARTH
| MARS
| JUPITER
| SATURN
| URANUS
| NEPTUNE deriving (Enum, Bounded, Show)
newtype Mass = Mass Double
newtype Radius = Radius Double
data PlanetStat =
PlanetStat {
mass :: Mass
, radius :: Radius
}
newtype SurfaceGravity = SurfaceGravity Double
newtype SurfaceWeight = SurfaceWeight Double
gConstant :: Double
gConstant = 6.67300E-11
planetStat :: Planet -> PlanetStat
planetStat MERCURY = PlanetStat (Mass 3.303e+23) (Radius 2.4397e6 )
planetStat VENUS = PlanetStat (Mass 4.869e+24) (Radius 6.0518e6 )
planetStat EARTH = PlanetStat (Mass 5.976e+24) (Radius 6.37814e6)
planetStat MARS = PlanetStat (Mass 6.421e+23) (Radius 3.3972e6 )
planetStat JUPITER = PlanetStat (Mass 1.9e+27 ) (Radius 7.1492e7 )
planetStat SATURN = PlanetStat (Mass 5.688e+26) (Radius 6.0268e7 )
planetStat URANUS = PlanetStat (Mass 8.686e+25) (Radius 2.5559e7 )
planetStat NEPTUNE = PlanetStat (Mass 1.024e+26) (Radius 2.4746e7 )
surfaceGravity :: Planet -> SurfaceGravity
surfaceGravity planet =
let (PlanetStat (Mass mass) (Radius radius)) = planetStat planet
in SurfaceGravity $ gConstant * mass / (radius * radius)
surfaceWeight :: Mass -> Planet -> SurfaceWeight
surfaceWeight (Mass otherMass) planet =
let (SurfaceGravity sg)= surfaceGravity planet
in SurfaceWeight $ otherMass * sg
runPlanets :: Double -> IO ()
runPlanets earthWeight =
let (SurfaceGravity earthSurfaceGravity) = surfaceGravity EARTH
massOnEarth :: Mass
massOnEarth = Mass $ earthWeight / earthSurfaceGravity
planetValues :: [Planet]
planetValues = [(minBound :: Planet) .. (maxBound :: Planet)]
printSurfaceWeight :: Planet -> SurfaceWeight -> String
printSurfaceWeight planet (SurfaceWeight sw) = "Your weight on " <> (show planet) <> " is " <> (show sw)
planetStatsStrings :: [String]
planetStatsStrings = (\p -> printSurfaceWeight p (surfaceWeight massOnEarth p)) <$> planetValues
in
traverse_ putStrLn planetStatsStringsThe source code for the example can be found on Github.
If there are any easier/better ways to encode this example in Haskell, please free to drop in comment.